Sunday 27 October 2013
Working with Integers
How many of us struggle with explaining integers? I know that I do. I find it most difficult to teach topics that are completely obvious to me, that I don't remember ever learning. So integers are right up there. Many years ago my friend, Tom Seidenberg, told me that he used the idea of a hot air balloon and sand bags. I ran with that and have been using it ever since. I am by no means saying that this is the best way to teach integers, but it does give students something concrete to hang on to. I must also say that my students have already been taught about integers, but many did not understand them the first time. This gives students a different way of thinking about integers. It takes a lot more than this to get them comfortable working with integers, but this is how I start.


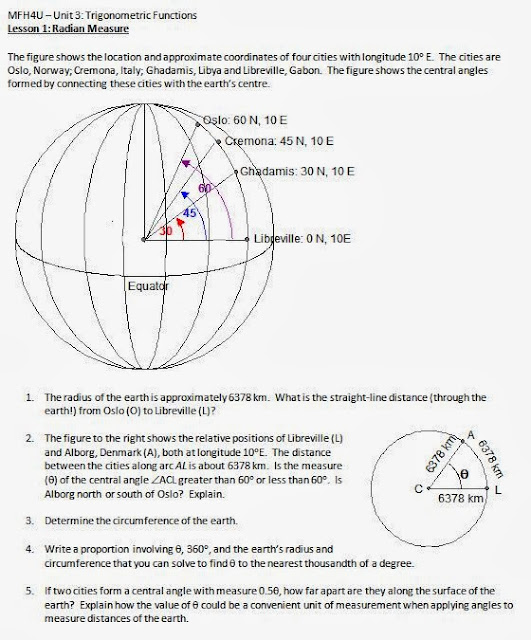
Introducing Radian Measure
In our curriculum, students learn all about right angle trig and sine and cosine laws in grade 10. In grade 11 they learn about the graphs of trig functions, all done in degrees. In grade 12 they are introduced to radian measure. I was introduced to this by Tom Seidenberg, so I give full credit to him as this may be straight from their materials. I like the way it sets up what 1 radian is and gives a context to arc length over radius.
Link to Word document
Link to Word document
Quadratic Headbanz
My grade 10 academic math class is filled with great kids. For the last week or so we have been exploring quadratics in vertex and factored form, with the help of Desmos. My students are pretty solid at going between equations and their graphs. On Friday, about half of my class was away on a history field trip. We finished some questions from the previous day but I didn't want to start anything new - I wanted to do something fun! At TMC13, Sam Shah organized a Rational Headbanz game for the pre-calc group and I thought I could modify it for quadratics.
With the help of my colleague, Michelle, we made 30 headbanz. We used coloured card stock, cut into rectangles with 2 slits cut along the sides to accommodate ribbon. I wrote the equations and this is how they turned out:
The kids were pretty excited to play. I like to have written instructions on top of what I say, so here is what they saw:
They each got a whiteboard to record their work. It was interesting to see them thinking about what to ask. Many started with "Am I in vertex form?" or "Am I in factored form?" but the poor student who had had a hard time getting good answers. They had to think about what questions to ask. The nice thing is that those who were struggling heard the questions others were asking them and were able to move forward. The trickiest part was with the value of h in
had a hard time getting good answers. They had to think about what questions to ask. The nice thing is that those who were struggling heard the questions others were asking them and were able to move forward. The trickiest part was with the value of h in
They would ask "Is my h value positive?" but then either interpret the answer incorrectly or not be sure whether the person they had asked truly understood what a positive h value meant.
They all figured out their equations and had fun doing so. And they want to play again next week when the whole class is there. I'll be happy to oblige.
Thanks, Sam, for the inspiration : )
With the help of my colleague, Michelle, we made 30 headbanz. We used coloured card stock, cut into rectangles with 2 slits cut along the sides to accommodate ribbon. I wrote the equations and this is how they turned out:
The kids were pretty excited to play. I like to have written instructions on top of what I say, so here is what they saw:
They each got a whiteboard to record their work. It was interesting to see them thinking about what to ask. Many started with "Am I in vertex form?" or "Am I in factored form?" but the poor student who had
 had a hard time getting good answers. They had to think about what questions to ask. The nice thing is that those who were struggling heard the questions others were asking them and were able to move forward. The trickiest part was with the value of h in
had a hard time getting good answers. They had to think about what questions to ask. The nice thing is that those who were struggling heard the questions others were asking them and were able to move forward. The trickiest part was with the value of h in They would ask "Is my h value positive?" but then either interpret the answer incorrectly or not be sure whether the person they had asked truly understood what a positive h value meant.
They all figured out their equations and had fun doing so. And they want to play again next week when the whole class is there. I'll be happy to oblige.
Thanks, Sam, for the inspiration : )
Subscribe to:
Posts (Atom)